Exploring Low Rank Adaptation with tinygrad
In this post, I'll highlight my project that implements Low Rank Adaptation (LoRA) using the tinygrad framework on a pre-trained model. The process involves simulating a pre-trained model with one epoch on the MNIST dataset, freezing the model parameters, identifying the worst classified digit, applying LoRA, and fine-tuning the model on training data filtered for that particular digit [1, 2]. The result shows improved performance on the identified digit without altering the frozen parameters.
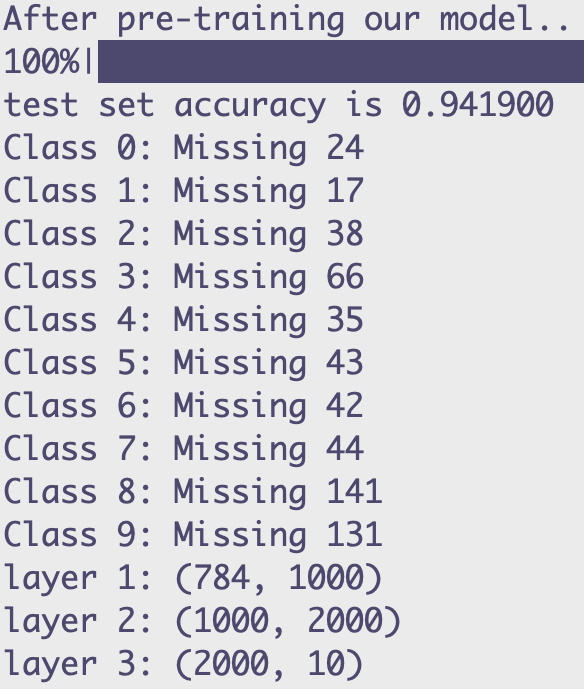
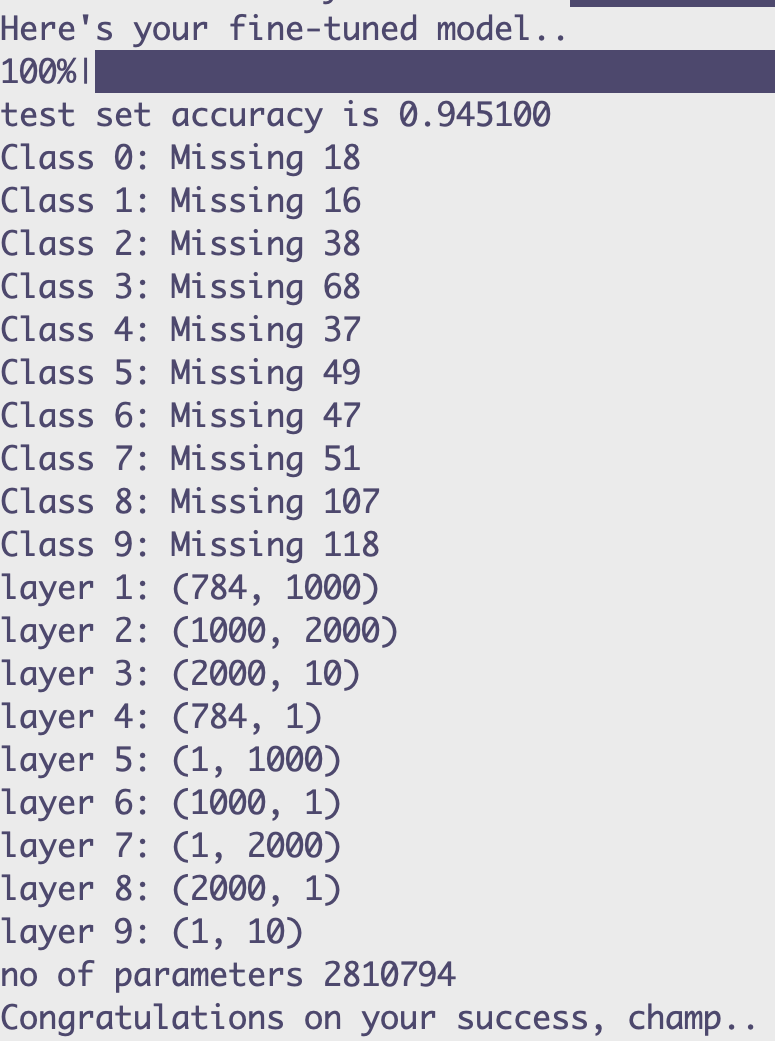 The LoRA parameters aren't technically considered "layers", just quicker to note it like that.
The LoRA parameters aren't technically considered "layers", just quicker to note it like that.
Introduction to MNIST, tinygrad and LoRA
MNIST is a dataset consiting of images of digits 0-9. The images are often used to predict what integer it is a drawing of. It's known for being small withonly 50K examples.
tinygrad is a minimal neural network framework known for its simplicity and ease of integration with new accelerators for both inference and training.
LoRA is a method aimed at efficient fine-tuning of pre-trained models by reducing the number of parameters involved in fine-tuning, thus potentially speeding up the process and saving resources.
There's a great image of LoRA on the first page of the original paper.
Benefits of tinygrad and LoRA
- Simplicity: tinygrad is simple, expressive, and pythonic which makes it easy to work with.
- Ease of Setup: tinygrad easy to set up with AMD GPUs, making it accessible for a broader range of developers, and making more competition for Nvidia.
- Efficiency: LoRA significantly reduces the number of parameters to be fine-tuned, making the process faster and less resource-intensive.
Implementing LoRA with tinygrad
The provided code snippet demonstrates the process:
- Simulating a Pre-trained Model: The model is simulated with one epoch on the MNIST dataset.
if __name__ == "__main__":
...
print("Simulating a pre-trained model, with one epoch..")
...
for epoch in range(1, epochs + 1):
train(model, train_data.X, train_data.Y, optimizer, steps=steps, lossfn=lossfn, BS=BS)
...
- Freezing Model Parameters: After simulation, the model parameters are frozen to preserve the pre-trained weights.
def loraize(model, rank=1, alpha=0.5):
...
for par in original_params:
par.requires_grad = False
...
- Identifying the Worst Classified Digit: The code identifies the digit 9 as the most poorly classified digit.
...
worst_class = max(mislabeled_counts, key=lambda k: mislabeled_counts[k])
print(f"Worst class: {worst_class}")
...
- Applying LoRA: The model is loraized to prepare for fine-tuning.
...
print("Lora-izing the model..")
lora_model = loraize(model)
setattr(lora_model, "forward", lambda x: lora_forward(lora_model, x))
...
- Fine-tuning the Model: The model is fine-tuned on training data filtered for digit 9.
...
print(f"Fine-tuning the worst class, {worst_class}..")
...
X_train, Y_train = filter_data_by_class(train_data.X, train_data.Y, worst_class)
filtered_data = Dataset(X=X_train, Y=Y_train)
...
for epoch in range(1, epochs + 1):
train(lora_model, filtered_data.X, filtered_data.Y, optimizer, steps=200, lossfn=lossfn, BS=BS)
...
Insights
It's observed that with a certain extent of fine-tuning, the model significantly improves in classifying the digit worst class. However, over fine-tuning could lead to the model performing worse on other digits. This balance is crucial for achieving an overall efficient fine-tuning.
References
- Inspiration from [1] & [2]
- [1] https://www.youtube.com/watch?v=PXWYUTMt-AU
- [2] https://colab.research.google.com/drive/13okPgkUeK8BrSMz5PXwQ_FXgUZgWxYLp